In Introducing the Western Music Language, we saw how we can derive the scale notes from the harmonics of one string. When considering subsequent divisions of a string by whole numbers, we actually observe a manifestation of the harmonic mediating proportion.

The series 1/2, 1/3, 1/4, 1/5, 1/6, ... is harmonic, ie b = 2ac/(a+c)

The notes that are created this way explain why the major chord is so pleasing to the ear. I did outline in a little textbook how we can derive all of the notes (chromatic scale) we use in western music just using this principle. However, when we look at a lot of ethnic music, we observe the 5 note pentatonic scale. This scale, by the way, is responsible for the blues and its numerous derivations.

The pentatonic scale can be wholly constructed using geometric proportion, and it can be derived by an even simpler method. To fully understand this process it is helpful to construct following contraption:

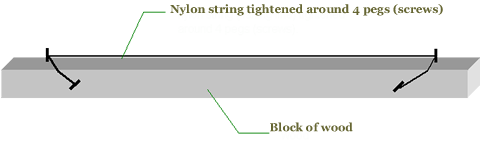
The string should be tightened as close as possible to the surface, but not so close that it buzzes when plucked. Aim for a good deep sound. The intervals (distances) between the notes (sounds) we will create are not dependent on the tightness of the string but on the relative subdivisions of the length of the string.

Note also that the 2 pegs on top are 81 cm apart. This is convenient because 81 is a multiple of 3 which will come in handy as we will see later on.

Now mark off the distances on your instrument as shown on the diagram below. Then press the string down with your left finger on each of these nodes, sounding the string with your right hand

If we press down halfway the string (at 40.5 cm), we will get the same note, but at a higher level. This is the octave. If we now press halfway the distance of this half (at 1/4), the same note will sound again at a higher level. We can theoretically go on like that ad infinitum, each time attaining the same note but at a higher level.
The image below is not to scale.

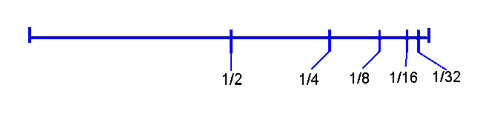
In other words, we are creating the following series:

Because each subsequent ratio is created by multiplying it by the same amount (in this case 1/2), the series is said to be geometric.

Ok, sounds good mathematically, but doesn't sound very exciting to our ears. Not a great variety of notes! What would the next logical step be? The same as above but using the next subdivision that is possible: division by 3. It turns out that the first subsequent divisions of a string by three creates our pentatonic scale. Though the principle is the same as above, in order for us to create a proper pentatonic scale, we also need to employ the important discovery we made above, namely that doubling or halving the length of a string produces the same note, be it on a different level

Why do we want to use this? Because we want to keep all our new-to-be-found notes within the same level. And in order to keep all our new-found notes within the octave, all we need to do is ensure that all the markations end up on the first half of the string. Note that this first half marks the octave (the same note on a higher level). Logically, all the notes that lie beyond this markation will repeat the ones below. Note: This is yet another example (metaphor) to depict the infinity of numbers on any length of string. Doing the following experiment will make this clear.

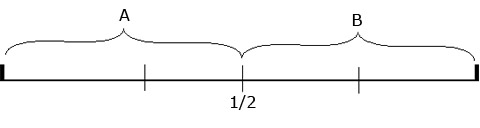
To avoid confusion, always press down with the LH and pluck the string with your RH. Now verify that all notes in B are present in A, but on higher levels.

Also note that we measure from the right, as we did in the experiment for deriving the octaves. This is important since we need to get the ratios from the string-length last obtained (by means of pressing down the string at those nodes).

Getting back to our intention of subsequently dividing the string by 3 ... mathematically,

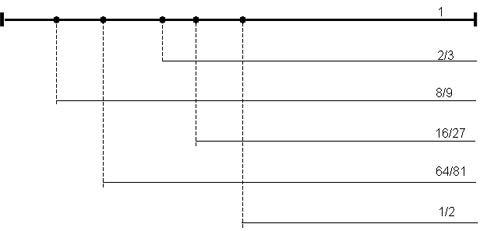
Now translate the found ratios so they are greater than 1/2, this way we remain within the octave: Remember, we can only multiple by multiples of 2 in order to obtain the same notes, be it on different levels:

The reasoning used for finding each of these notes is as follows (using the example of 1/9):

• 1/9 is smaller than 1/2, therefore multiply with 2
• 2/9 is smaller than 1/2, therefore multiply with 2 again
• 4/9 is smaller than 1/2, therefore multiply with 2 a third time
• 8/9 is greater than 1/2, therefore this is our note.

Do this with the other ratios as well, and sito, there's our five notes (including the full length, do): do, sol, re, la, mi

All we need to do now is to convert it to our instrument. Since the string is 81 cm long, we use the found ratios to calculate the distances:

• Subsequent divisions by half creates a string with the same notes as the fundamental note. As the lengths get smaller, the distances required are smaller. This is the concept of the logarithm.
• The left (top) part of the ratios are multiples of 2, the right (bottom) part of the ratios multiples of 3 (disregarding the octave).
• For those of you that know of the circle of fifths in music theory, note that all we have done is create the first subsequent fifths.
• Think of the mathematical concept of recursion and recognise it in the string.
• The table below shows what would happen if we follow the above reasoning for division by 5.

The following tables are copied from a MS Excel file I wrote. It calculates all the fields given a particular string length.

The example shows the values for a string length of 100. However, if you download the file to your computer you can manipulate it yourself by 'inputting' any value of string length you want. The tables will update accordingly. I inserted some comments before each table.

Download the Excel file here

Input string length: 100.00 from bridge (right)

Divisor: five

This is just to show what happens when we take the next possible subdivision, subsequent division by five. Playing these intervals gives an Eastern type of scale, very pleasing to the ear, but not representative of the western scale.

circle of 5ths

This is the one we've worked out above. I stopped the subdivision because excel doesn't show ratios containing numbers with more than 3 digits.

chromatic scale

This is the standard tuning used for all modern instruments these days, because it greatly facilitates tuning instruments. It also enables us to play in all 12 keys. The formula used has been described somewhere earlier in this article.

Own system

Shows the scale obtained from my book 'Introducing the western music language'. Note that it shows exactly the same ratios as those used in tempered tuning.

Classic tempered tuning

This is taken from a book on piano tuning and is regarded as the standard tuning. It is possibly the most harmonious representation of what happens when a string is plucked. Note that the missing notes f# and bb are prominent in other tables.

harmonic

The first two intervals are very standard, but the series soon gets out of step compared with our chromatic scale, which we use as a standard.

circle of fifths

A completed version of the second table. The 'difference in ratio' column shows the difference between this on and the chromatic (12√) one. This table helps us to connect 2^(x/12) to the circle of fifths. Get exact measurements and find out the rate at which they are out. (Pythagoras's comma).

The 2 in the formula stems from the fact that we need a length of two units since we can only use half of a unit length to get our scale. Any notes lying outside this half is just repeating these notes. So to make things as abstract as possible, we take this half as unit, and therefore the whole string as 2 units.
The 12^th root accounts for the fact that we need to multiply something with itself 12 times to get 2. This means that lowering a tone equals to dividing the present length by 12√2, and raising a tone equals to multiplying the present length by 12√2.
Note also that each note on this string keeps its identity when successively multiplied by 2, ie by multiples of 2. The binary aspect is very strong.

The next strong aspect is the ternary one. The whole system is really based on an interaction of these 2 principles, ie the binary and ternary. The ternary principle creates new notes. The binary brings them to a particular level

Note that after 12 iterations, we derive a ratio of 0.98654... This is very close to the original string ratio for a full length, 1. The difference between the two has been termed the Pytagorian comma. For all practical reasons, the circle of 12 is said to be repeating.

An interesting point that crops up when we compare the two ratios is the constant approximity of the two. One is always a little greater than the other, but there does not seem to be a fixed ratio that links them both.

Represents both the circle of fifths and chromatic mathematically.

Always +7 , -5. Starting from 0, until 12 reached, then it starts (on the fifth, g) on 1. Significantly, the power ends on 12 (3^12).

always +11, -8. starting from 0, until 20 is reached, then it starts (on the fifth, g) on 1. It ends on 19.

Also, adding both multiples gives the series 0, 18, 5, 23, 10, 28, 15. Again, this reveals an order: +18, -13 from 0 until the fifth, and then it starts from 2.

Take the e note:

2(2^6/3^4)
(2^(8/12) = 2^(2/3))

Interaction of 2 and 3 only gives the circle of fifths.

The reverse of all the ratios gives the same result, but starting from the octave.