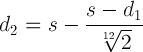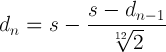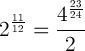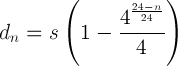This section actually belongs to Music, Scales and Tuning and Constructing Scales in this same folder, however I intend to re-organise those 2 pages in the near future to make them more coherent.

I just need to build on one particular result we obtained, namely that to decrease the pitch by half a step, we need to increase the string length by

.

This sort of makes sense intuitively: The 2 in the formula stems from the fact that the octave is halfway the string, and the 12 notes lie within the one octave. So we regard the whole string as 2 units. The 12th root accounts for the fact that we need to multiply something with itself 12 times to get 2. This means that lowering a tone equals to multiplying the present length by 12√2, and raising a tone equals to dividing the present length by 12√2. As I said, this only makes sense intuitively, read the above mentioned pages if you want the mathematics.

We will discuss 2 methods to construct a fretboard, both of which are build upon the above finding.

This method calculates each distance depending on the previously obtained result. The only factor that needs to be known is the total length between the bridge and the nut, referred to as the Scale. It's not a big step from the above equation to the first one below.

	d1 is the distance from the nut to the first fret s is the Scale, which is the distance between the bridge and nut
	d2 is the distance from the nut to the second fret note that this result depends on the previously acquired value for d1
	general version for the recursive equation n is the fret number - e.g. for the 11th fret, replace n with 11

This equation doesn't need previously calculated results, it stands on its own. It too is derived from the 12√2 formula stated at the beginning.

	d1 is the distance from the nut to the first fret s is the Scale, which is the distance between the bridge and nut note that a power of 1/12 is the same as the 12√2, it's just written differently. Therefore 2 to the power of 11/12 is the same as 12√211(the 12th root of 2 to the power of 11)
	d2 is the distance from the nut to the second fret note that the values decrease as the fret number increases
	general version derived from the 2 equations above n is the fret number

There is an interesting limitation in this general equation: Once we reach fret 12, the whole factor containing the power becomes 1, and the distance for fret 12 will be halfway the length (remember how we described this in the intuitive explanation for the 12th root of 2). Note that no such limitation exist in the recursive method even though it is based on the same 12th root of 2 equation.

Luckily we can use simple algebra to convert our 12th root expression so that it can handle 2 octaves (24 frets) instead of 12. For example,

Using this knowledge, we can transform our last obtained equation that was limited to 12 frets to one that allows 24 frets (after a little rework).

We can use any one of the 2 derived equations to construct a fretboard. Only the Scale needs to be known. You can find scales for particular instruments in various manufacturer's datasheets on the net.

I created a little spreadsheet to assist calculation, it uses both equations - the results of which are exactly the same. Just enter the Scale value (red number) and the fret distances will update.