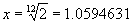This page contains snippets and ideas collected over some time. It mainly covers some technical aspects of sound, forming scales by using string ratios, and tuning techniques.
Another article in this category Constructing Scales follows a more coherent reasoning in the quest of understanding how our musical scales are constructed.

The mechanical operation of the ear is well understood; however, the perception of sound involves complex neurological processing of information that is not yet fully explained. An example is the use of earphones. The speaker can not efficiently produce any sound with a wavelength much larger than the diameter of the speaker. Earphone speakers are too small to reproduce the low frequency fundamentals of many musical sounds, although they may accurately reproduce the overtones. Nevertheless, music heard on earphones sounds as though the fundamental were present because the brain, recognising the harmonics, effectively supplies the fundamental.

Ultrasound sources are usually crystals that are either piezoelectric or magnetostrictive. A piezoelectric crystal is one in which an applied electric field alters the molecular positions, producing stresses in the crystal. If the applied field is periodic, the crystal vibrates, producing sound. Magnetostrictive materials exhibit similar behaviour in an applied magnetic field. Both types of transducers also act as receivers, since the mechanical vibrations produce electric and magnetic fields that can be detected and used to monitor incoming sound waves.

Note all pitches are derived from the one string, using whole number ratios. These frequencies (or pitches or tones) occur naturally in all stretched strings. They are therefore in harmony with nature, hence the term harmonics.

Pitches played together produce the Major chord Do - Mi - Sol

In the above we used ratios based on the fundamental string (note) Do, which was set to unity (1). But we can derive, just by using the information we already have, another set of ratios, namely the ratios between each successive pair of notes. This will determine the interval between these pairs. To do this, we need to make one of each pair unity. The first pair we encounter in the above list already has the first one set to unity. So we can say our first interval has the ratio of 1 : 2.

The next pair of ratios are 1 : 2 and 1 : 3. The interval between this (which is actually a ratio of ratios) can be calculated as follows:

Make the first one unity and remember the factor needed to make it unity. ie we need to multiply the 1 : 2 by 2 to get unity. This factor 2 needs to be made common to both. So, to retain the interval we then need to multiply 1 : 3 by 2 also ie. 2 : 3.

The above argument is made for the other pairs too, this way we can expand our table above:

x¹² = 2

To raise note by half a tone: multiply note's frequency by x

To lower note by half a tone: divide note's frequency by x

This knowledge is used by piano tuners for tempering the piano scale

Ascertain what the vibration number of the exact 5th would be. Find the difference between this and the tempered fifth. Multiply the difference by 3. This gives you the number of beats. (A variation of 1 vibration per second in the 5th causes 3 beats per second)

Example

The beats one hears is due to the clash between the 2nd harmonic on the root c, which is the fifth, and the out-of-tune, tempered g.

Treble tuning

• First Octave
• Tune octaves
• Test by fifths and chords above
• Tune octaves
• Listen for pitch rather than beats

Bass tuning

• listen for beats only in the octaves
• Watch the false waves (metallic timbre)