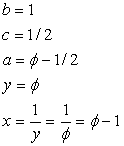The web has countless webpages devoted to PHI, the Golden Proportion (sometimes called the Golden Mean). All these concepts are related to the simple series 1, 1, 2, 3, 5, 8, 13, 21, ... i.e. the infamous Fibonacci Series.

The series in itself is not such a wonderful thing; in fact, it stands out in its simplicity. However, the mathematics it produces is very interesting.

The amazing thing about Φ is that it can be explored using many different lines of thought, connecting seemingly unrelated ideas. My contribution to this subject is in revealing some lesser known aspects about Φ.

The whole of the Fibonacci series is built on itself. A sequence like 1, 2, 3, 4, 5, ... always needs 1 to increment its last attained number. This 1 is like an outsider that constantly needs to be fetched.

Another example is a series like 3, 6, 12, 24, 48, ... This series always needs the constant 2 to multiply the last number attained.

However, 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci series) simply takes the former two numbers and adds them.

An imaginary robot walking along the series only needs to know how to add numbers. It does not need to store any outside information, like the number 1 or 2 in the first two series. Nor does it need to jump from here to there. It actually can grow the series using the least amount of information necessary.

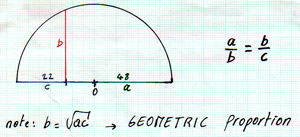
Taking 2 consecutive numbers in the series and dividing the larger with the smaller one gives you a number that approaches Φ (1.6180399 ...). The further you go up the Fibonacci series, the closer this number approaches Φ. Since it can't be expressed with any one particular ratio, it is called irrational.

Similar sequences can be made by, say starting with two: 2, 2, 4, 6, 10, 16, ...

These alternative sequences have similar properties and also occur in nature. But the 0,1 Fibonacci series is the most fundamental one.

Information in this section is borrowed and adapted from Ian Stewart's excellent book Life's other secret (ISBN 0-713-99161-5)

Plants begin their existence as seeds that germinate to put out many tiny roots which grow downwards into the ground, and also a single shoot which grows upwards into the sunlight. If you look at the tip of this single shoot under a microscope, you can see the bits and pieces from which all the main features develop - leaves, petals, sepals, florets, etc

At the center of the tip is a circular region of tissue called the apex. Around the apex, one by one, tiny lumps form, called primordia.

Each primordium migrates away from the apex, or more accurately, the apex grows away from the lump, leaving it behind. Eventually, the lump develops into a leaf, petal or the like. Primordia that pop into existence earlier will migrate further.

Figure: Primordia numbered in order of appearance

Figure: Spacing of primordia shown in a cross section of a bud

It turns out that the angle (divergence angle) between successive primordia coming into existence is very close to 137.5° (2.4 radians).

360° - (Φ * 360°) = 137.5°

This angle, also called the golden angle, turns out to be the only angle at which seeds can pack without gaps.

Figure: Packings created by divergence angles of (a) 137.3°, (b) 137.5° (golden angle) and (c) 137.6°

So in that sense the golden angle can be seen as a consequence of sensible dynamics.

Looking at the figure above, assume a divergence angle of 180°. This means that successive elements would be arranged along two radial lines, clearly not filling in all available spaces ... In fact, any divergence angle that is a rational multiple of 360° will give radial lines, ie for a divergence angle of 360 * p/q degrees, we will get q radial lines.

To get efficient filling you need a divergence angle that is an irrational multiple of 360°. In fact you ought to use the most irrational number possible. And number theorists have long known that the most irrational number is Φ , the golden number ...

This is why: We have already touched upon the fact that Φ is the limit of the sequence 2/3, 3/5, 5/8, 8/13, 13/21, ...

Each ratio in the series is a rational approximation to Φ. Moving along the series, they get closer and closer to it but never equal Φ exactly. Now we can measure how irrational Φ is by seeing how quickly the differences between these fractions and Φ shrink towards zero. What the number theorists proved is that for Φ, the differences shrink more slowly than they do for any other irrational number.

In other words, Φ is badly approximated by rationals. If you quantify the degree of approximation in a reasonable way, it's the worst of them all.

Φ is much lesser known than π (PI) but by no means less important. While π is used in important equations, for some reason, Φ isn't (as far as I know). This probably adds to the mystique so often attributed to Φ.
The only reason I can think of is that Φ doesn't represent a relationship between 2 fundamental entities (like π does with radius and circumference), but is a fundamental entity in itself by the fact that it represents the simplest type of proportion possible. To explore this a bit further we need know the difference between ratio and proportion:

A ratio is a comparison of 2 different quantities or qualities, i.e. a/b

A proportion is a relationship of equivalence between 2 ratios. There are 3 types of proportion:

4 term proportion

• The diagonal determines the proportion
• Also called "discontinuous proportion"
• 3 terms need to be known

3 term proportion

• The circle determines the proportion
• Also called "continuous proportion"
• 2 terms need to be known

2 term proportion

• This is a special case of 3 term proportion whereby one of the terms is the sum of the other 2. This occurs when the smaller term is to the larger term as the larger term is to the smaller plus the larger.
• Only 1 term needs to be known.

Note that in its simplest form, if b in the last figure equals 1, then

a + b = (SQRT 5 + 1) / 2 = Φ

This relationship is, I think, very important, and I haven't seen it mentioned anywhere else. We tend to think that the fact our counting system uses base 10 is rather accidental and possibly due to the fact that we have 10 fingers. Indeed, other base systems, such as binary and hexadecimal seem to work just as well, at least as far as computers are concerned. However there is something more fundamental to the number 10 ....

I start with the following hypothesis:

In its purest mathematical form, PHI is the result of an interaction of 2 fundamental principles: HALF-NESS and TEN-FOLDNESS

So far, we have established that there is a unique situation in which a proportion can be expressed, using only 2 terms. There is more to be found in this diagram:

Let b be unity, then

Note in particular the right-angled triangle in which c is exactly HALF of b. In this situation, the hypotenuse a will be related to Φ.

Now look at what happens when we have 2 such contraptions in one circle. Note that by lining up the hypotenuse to the specific angle of 1/10^th of the full circle (36 deg), the projections (from intersecting points) on to the x axis line up neatly and divide the x axis into 10 almost equal parts.

This also leads to an interesting relationship with π

Following figure also illustrates the relationship with π from a different perspective

A closer look at the actual triangle

Here's a spreadsheet (in .xls format) that shows the fibonacci series in different number systems (different bases). It also shows the modulus (rest obtained when dividing by the base). Note that the Modulus 5 is the only one that returns to 0 every 5 numbers. Interestingly, the 10^th number is 55.

Download or open this document from here

Lastly, I include some diagrams of interest here

More Φ relationships in the right-angled triangle - 1

More Φ relationships in the right-angled triangle - 2

Φ relationships in the Pentagon

Fibonacci relations expressed in a Composite Fraction