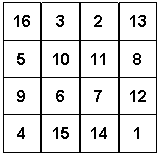
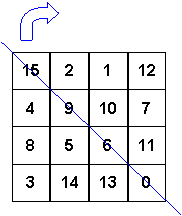
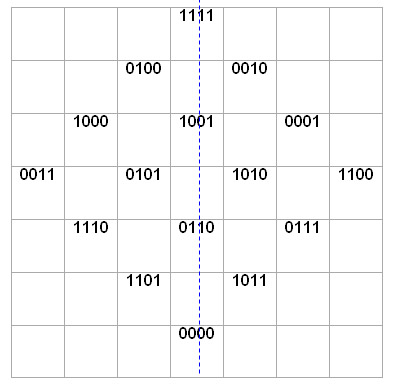
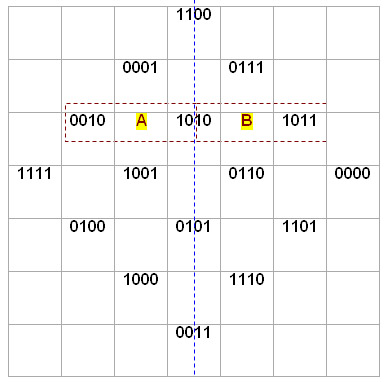
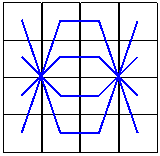
This magic square has some truly extraordinary characteristics, bordering on the incredible. Mark Collins (Madison, Wisconsin): "I believe this magic square is an archetype as rich in meaning and mysticism as the I Ching. I believe it is a mathematical and visual representation of nature's origami - as beautiful as a photon of light."

• The 2 central numbers in the bottom row read 1514, the year Durer made the etching.
• In the vertical, the horizontal, and the 2 diagonal directions, the numbers sum to 34.
• The sum of the numbers of the corner squares is 34.
• The sum of the small central square is 34.
• The sum of the remaining numbers is 68 = 2 x 34.
• The sum of the outer squares is 102 = 3 x 34.

1. Convert to hexadecimal form (written in binary): We take away 1 from each number, thus deriving the standard binary notation of the first 16 numbers, starting from binary 0 to binary 15. Note that all the characteristics of the square are still present. Only now all the calculations add to 30, not 34.



2. Rotate the square 45 degrees clockwise.

   




3. Draw a center line through the table of numbers thus obtained. The resulting pattern has a vertical mirror plane down its center.

   

We can also derive the number's inverse complements by turning the said square counter-clockwise 45 degrees

For example, in the table above, add A to B's inverse:

  0 0 1 0 1 0
+1 1 0 1 0 1
  ------------
  1 1 1 1 1 1

A mitosis-like diagram can be created by connecting successive sequences of 4 numbers: Connect 0, 1, 2, 3 and 4, 5, 6, 7 and 8, 9, 10, 11 and 12, 13, 14, 15

Connecting the points making the sequence 0, 3, 6, 9, 12, 15 reveals a symmetric - inverse graph. Starting from both ends, the line makes opposite moves.