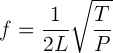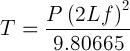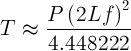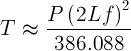Calculating the tension exerted by strings is a crucial factor in determining string gauges for musical string instruments. There is much confusion regarding unit and unit conversion terminology in the equation for string tension. This writing attempts to put some order into this.

The relation describing the physics in a string is given by the following equation

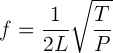
• f = frequency - in Hz or cycles/second
• L = string length (between nut and bridge) - in meters
• T = Tension (Force) on the string - in Newtons
• P = Unit Weight of the string - in Kg/m

Reworking this equation to get the Tension on the string:

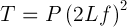
It is interesting to note that the Force or Tension on the string is the accumulation (multiplications) of all the factors in the relation.

This is the fundamental equation describing the tension on a string. The confusion arises when adapting this equation for different units. Tension is often mistakenly given in Kg or Pound. This should be kgf or kg_F (Kilogram force) and lb_f (Pound force). To convert Newtons into Kilogram force, use the following unit conversion:

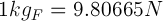
Hence the fundamental equation can be written as

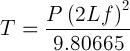
• f = frequency - in Hz or cycles/second
• L = string length (between nut and bridge) - in meters
• T = Tension (Force) on the string - in kg_F (Kilogram force)
• P = Unit Weight of the string - in Kg/m

To convert Newtons into Pound force, use the unit conversion

Therefore the fundamental equation can be rewritten as

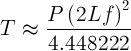
• f = frequency - in Hz or cycles/second
• L = string length (between nut and bridge) - in meters
• T = Tension (Force) on the string - in lb_f (Pound force)
• P = Unit Weight of the string - in Kg/m

The Unit Weight (P) can be derived from manufacturers' datasheets, such as D'Addario's datasheet. However you'll often find it given in Pounds per linear Inch. Hence we need an equation that allows for Imperial units. To derive this we need to take the standard equation and multiply each factor with the amount required for the imperial unit. The conversion factors are

• 1 Newton = 1/4.448222 = 0.224809 lb_f
• 1 kg = 2.204622 lb
• 1 m = 39.370079 inch

Inserting these conversion factors in the standard equation gives the following proportional relationship:

Note that I left out the constant 2 and the f factor because they are the same in imperial (the conversion factors would be 1). Solving this relation gives

Hence the final equation using imperial units:

• f = frequency - in Hz or cycles/second
• L = string length (between nut and bridge) - in inches
• T = Tension (Force) on the string - in lb_f (Pound force)
• P = Unit Weight of the string - in pounds/linear inch

The above derived value of 386.088 is somewhat different from the value of 386.4 given on D'Addario's Strings website. Since tension is a string manufacturer's business I don't doubt this value. This is probably due to them taking imperfections such as stiffness into account. After some enquiries regarding this discrepancy, I received an email from R.M. Mottola, a stringed instrument designer, with the following explanation ...

My suspicion is that they took this from a more accurate solution to the governing wave equation, one that considers inharmonicity in real strings, and thus results in higher freq for given tension. These solutions generally taken the form of polynomial series with the first term being that for an ideal string, the formula you use in your derivation. From a practical perspective one must decide how many terms one needs to use to get acceptable accuracy. But needless to say the more additional terms are used, the lower the value of the denominator constant will be.