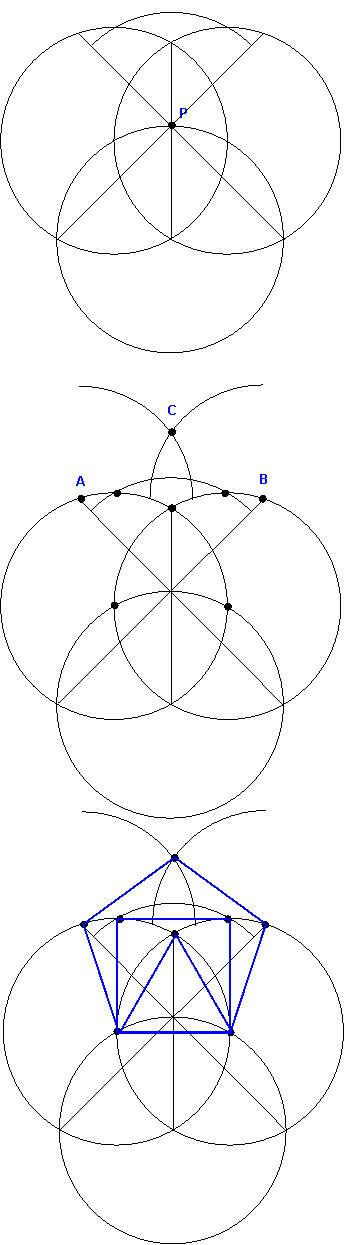
Introduction
The act of constructing pentagons is quite revealing, it makes one think back to the ancient Greek civilisation where philosophers like Plato and Pythagoras used geometry to explain and visualise fundamental concepts.
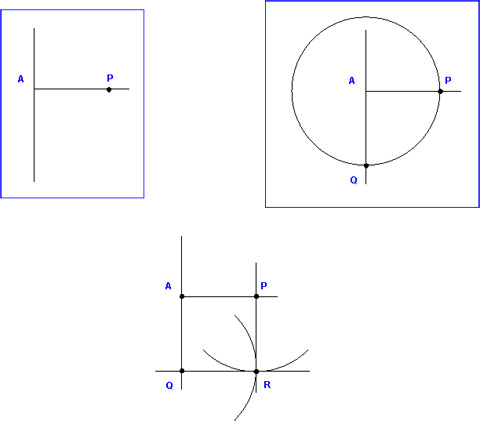
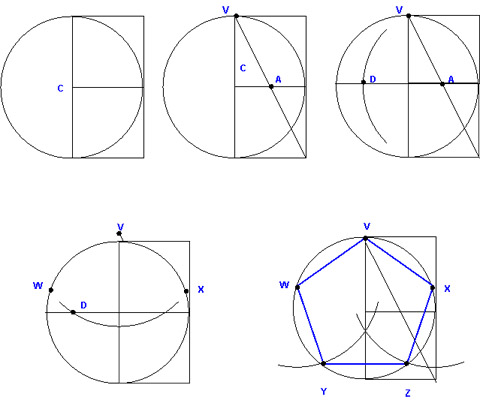
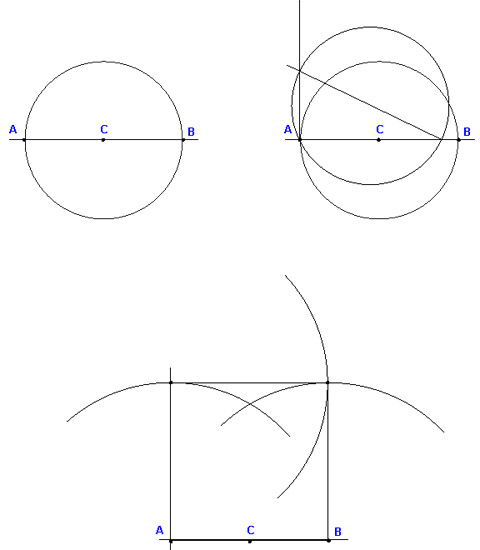
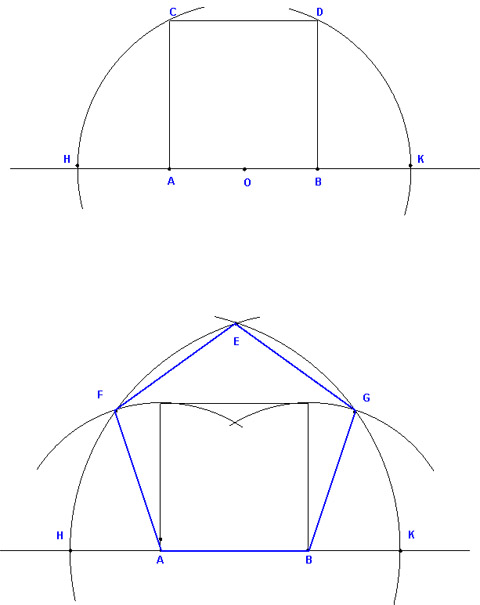
I will describe 3 systems of construction, all using only a set of compasses and a ruler. No metric measurements need to be made. Before describing the first method however, we need to be able to construct a right angle and a square.
The relationship between PHI and the Pentagon is touched upon in the article PHI elsewhere in this category.