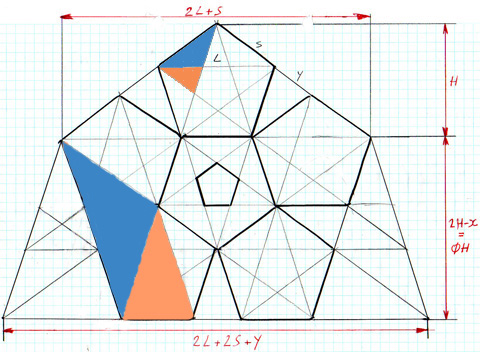
The Penrose Tiles illustrate that mathematics can indeed be beautiful. The tiles are essentially the two types of triangles that can be found in the Pentagon (coloured blue and orange in the figure below). See how these triangles occur on different scales within the one pentagon. This is because the cross-lines of one pentagon creates a little pentagon within, whose cross-lines in turn creates a smaller one again etc, hinting to an inherent recursive nature.

It can be seen from the figure that the larger triangles can be made up from smaller triangles. In other words, having many copies of just 2 triangle enables you to construct the amazing patterns with what are called, the Penrose tiles. I myself have dabbled a little in this and have come up with, what I believe to be, some creative results.

First I had to come up with a pattern in order to cut out the necessary triangles with efficiency:

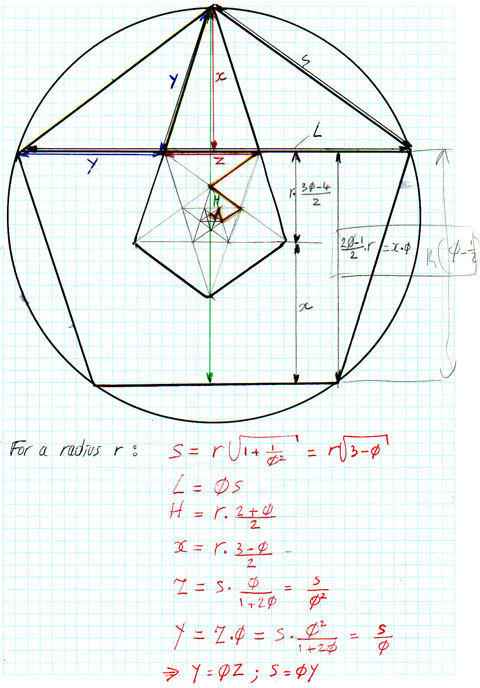
Next I needed some equations in order to draw them accurately. The figure below also accentuates the recursive nature within a pentagon with the yellow-red zig-zag line.

Note also the extensive occurance of PHI (Φ) in the equations.

Following are some examples of patterns in the making. Even though these patterns solely consist of 2 types of triangles, they have an organic look about them ...

Following is based on pages 562 - 566 from Roger Penrose's book: The Emperor's new mind. ISBN 0-19-286198-0

The only rational symmetries that are allowed for a crystalline pattern are twofold, threefold, fourfold, and sixfold. (Crystalline patterns have a translational symmetry)

...However 'quasi-periodic' symmetry can be achieved by using 5-fold symmetry (R.Penrose tiles).

If we imagine a substance with its atoms at the vertices of a 5-fold symmetric figure, it would appear to be crystalline. Also, the symmetry would have to extend in 3 dimensions, causing a icosahedral (20-plane phases) symmetry

Such substances were discovered (a phase of an aluminium-manganese alloy).

The remarkable feature of these crystals is that in assembling the patterns, it is necessary , from time to time, to examine the state of the pattern, many atoms away from the point of assembly.

The way that I picture this growth taking place is that, instead of having atoms coming individually and attaching themselves (like what happens in crystals), one must consider an evolving quantum linear superposition of many different alternative arrangements of attaching atoms. Indeed this is what quantum mechanics tells us must be occurring. There is not just one thing that happens; many atomic alternative atomic arrangements must coexist in complex linear superposition.

Normally, when nature seeks out a crystalline configuration, she is searching for a configuration of lowest energy. The same is true for quasi-crystal growth, the difference being that this state of lowest energy is much more difficult to find. The best configuration can only be discovered by a cooperative effort among a large number of atoms all at once.

Many different arrangements are tried simultaneously. The selection of an appropriate solution to the minimising problem must be achieved as the one-graviton criterion (or appropriate alternative) is reached - which would presumably only occur when the physical conditions are just right.